Thursday, November 16, 2006
Basic mathematical symbols
Symbol | Name | Explanation | Examples |
|---|---|---|---|
| Read as | |||
| Category | |||
| = | equality | x = y means x and y represent the same thing or value. | 1 + 1 = 2 |
| is equal to; equals | |||
| everywhere | |||
| ≠ <> != | inequation | x ≠ y means that x and y do not represent the same thing or value. (The symbols != and <> are primarily from computer science. They are avoided in mathematical texts.) | 1 ≠ 2 |
| is not equal to; does not equal | |||
| everywhere | |||
| < > ≪ ≫ | strict inequality | x < y means x is less than y. x > y means x is greater than y. x ≪ y means x is much less than y. x ≫ y means x is much greater than y. | 3 <> 4. 0.003 ≪ 1000000 |
| is less than, is greater than, is much less than, is much greater than | |||
| order theory | |||
| ≤ ≥ | inequality | x ≤ y means x is less than or equal to y. x ≥ y means x is greater than or equal to y. | 3 ≤ 4 and 5 ≤ 5 5 ≥ 4 and 5 ≥ 5 |
| is less than or equal to, is greater than or equal to | |||
| order theory | |||
| ∝ | proportionality | y ∝ x means that y = kx for some constant k. | if y = 2x, then y ∝ x |
| is proportional to | |||
| everywhere | |||
| + | addition | 4 + 6 means the sum of 4 and 6. | 2 + 7 = 9 |
| plus | |||
| arithmetic | |||
| disjoint union | A1 + A2 means the disjoint union of sets A1 and A2. | A1 = {1, 2, 3, 4} ∧ A2 = {2, 4, 5, 7} ⇒ A1 + A2 = {(1,1), (2,1), (3,1), (4,1), (2,2), (4,2), (5,2), (7,2)} | |
| the disjoint union of ... and ... | |||
| set theory | |||
| − | subtraction | 9 − 4 means the subtraction of 4 from 9. | 8 − 3 = 5 |
| minus | |||
| arithmetic | |||
| negative sign | −3 means the negative of the number 3. | −(−5) = 5 | |
| negative ; minus | |||
| arithmetic | |||
| set-theoretic complement | A − B means the set that contains all the elements of A that are not in B. | {1,2,4} − {1,3,4} = {2} | |
| minus; without | |||
| set theory | |||
| × | multiplication | 3 × 4 means the multiplication of 3 by 4. | 7 × 8 = 56 |
| times | |||
| arithmetic | |||
| Cartesian product | X×Y means the set of all ordered pairs with the first element of each pair selected from X and the second element selected from Y. | {1,2} × {3,4} = {(1,3),(1,4),(2,3),(2,4)} | |
| the Cartesian product of ... and ...; the direct product of ... and ... | |||
| set theory | |||
| cross product | u × v means the cross product of vectors u and v | (1,2,5) × (3,4,−1) = (−22, 16, − 2) | |
| cross | |||
| vector algebra | |||
| · | multiplication | 3 · 4 means the multiplication of 3 by 4. | 7 · 8 = 56 |
| times | |||
| arithmetic | |||
| dot product | u · v means the dot product of vectors u and v | (1,2,5) · (3,4,−1) = 6 | |
| dot | |||
| vector algebra | |||
| ÷ ⁄ | division | 6 ÷ 3 or 6 ⁄ 3 means the division of 6 by 3. | 2 ÷ 4 = .5 12 ⁄ 4 = 3 |
| divided by | |||
| arithmetic | |||
| ± | plus-minus | 6 ± 3 means both 6 + 3 and 6 - 3. | The equation x = 5 ± √4, has two solutions, x = 7 and x = 3. |
| plus or minus | |||
| arithmetic | |||
| plus-minus | 10 ± 2 or eqivalently 10 ± 20% means the range from 10 − 2 to 10 + 2. | If a = 100 ± 1 mm, then a is ≥ 99 mm and ≤ 101 mm. | |
| plus or minus | |||
| measurment | |||
| ∓ | minus-plus | 6 ± (3 ∓ 5) means both 6 + (3 - 5) and 6 - (3 + 5). | cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y). |
| minus or plus | |||
| arithmetic | |||
| √ | square root | √x means the positive number whose square is x. | √4 = 2 |
| the principal square root of; square root | |||
| real numbers | |||
| complex square root | if z = r exp(iφ) is represented in polar coordinates with -π < φ ≤ π, then √z = √r exp(i φ/2). | √(-1) = i | |
| the complex square root of … square root | |||
| complex numbers | |||
| |…| | absolute value | |x| means the distance along the real line (or across the complex plane) between x and zero. | |3| = 3 |–5| = |5| | i | = 1 | 3 + 4i | = 5 |
| absolute value of | |||
| numbers | |||
| Euclidean distance | |x – y| means the Euclidean distance between x and y. | For x = (1,1), and y = (4,5), |x – y| = √([1–4]2 + [1–5]2) = 5 | |
| Euclidean distance between; Euclidean norm of | |||
| Geometry | |||
| | | divides | A single vertical bar is used to denote divisibility. a|b means a divides b. | Since 15 = 3×5, it is true that 3|15 and 5|15. |
| divides | |||
| Number Theory | |||
| ! | factorial | n ! is the product 1 × 2× ... × n. | 4! = 1 × 2 × 3 × 4 = 24 |
| factorial | |||
| combinatorics | |||
| T | transpose | Swap rows for columns | Aij = (AT)ji |
| transpose | |||
| matrix operations | |||
| ~ | probability distribution | X ~ D, means the random variable X has the probability distribution D. | X ~ N(0,1), the standard normal distribution |
| has distribution | |||
| statistics | |||
| ⇒ → ⊃ | material implication | A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B. → may mean the same as ⇒, or it may have the meaning for functions given below. ⊃ may mean the same as ⇒, or it may have the meaning for superset given below. | x = 2 ⇒ x2 = 4 is true, but x2 = 4 ⇒ x = 2 is in general false (since x could be −2). |
| implies; if … then | |||
| propositional logic | |||
| ⇔ ↔ | material equivalence | A ⇔ B means A is true if B is true and A is false if B is false. | x + 5 = y +2 ⇔ x + 3 = y |
| if and only if; iff | |||
| propositional logic | |||
| ¬ ˜ | logical negation | The statement ¬A is true if and only if A is false. A slash placed through another operator is the same as "¬" placed in front. (The symbol ~ has many other uses, so ¬ or the slash notation is preferred.) | ¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y) |
| not | |||
| propositional logic | |||
| ∧ | logical conjunction or meet in a lattice | The statement A ∧ B is true if A and B are both true; else it is false. For functions A(x) and B(x), A(x) ∧ B(x) is used to mean min(A(x), B(x)). | n <>n >2 ⇔ n = 3 when n is a natural number. |
| and; min | |||
| propositional logic, lattice theory | |||
| ∨ | logical disjunction or join in a lattice | The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false. For functions A(x) and B(x), A(x) ∨ B(x) is used to mean max(A(x), B(x)). | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 when n is a natural number. |
| or; max | |||
| propositional logic, lattice theory | |||
⊕ ⊻ | exclusive or | The statement A ⊕ B is true when either A or B, but not both, are true. A ⊻ B means the same. | (¬A) ⊕ A is always true, A ⊕ A is always false. |
| xor | |||
| propositional logic, Boolean algebra | |||
| direct sum | The direct sum is a special way of combining several one modules into one general module (the symbol ⊕ is used, ⊻ is only for logic). | Most commonly, for vector spaces U, V, and W, the following consequence is used: U = V ⊕ W ⇔ (U = V + W) ∧ (V ∩ W = ∅) | |
| direct sum of | |||
| Abstract algebra | |||
| ∀ | universal quantification | ∀ x: P(x) means P(x) is true for all x. | ∀ n ∈ ℕ: n2 ≥ n. |
| for all; for any; for each | |||
| predicate logic | |||
| ∃ | existential quantification | ∃ x: P(x) means there is at least one x such that P(x) is true. | ∃ n ∈ ℕ: n is even. |
| there exists | |||
| predicate logic | |||
| ∃! | uniqueness quantification | ∃! x: P(x) means there is exactly one x such that P(x) is true. | ∃! n ∈ ℕ: n + 5 = 2n. |
| there exists exactly one | |||
| predicate logic | |||
| := ≡ :⇔ | definition | x := y or x ≡ y means x is defined to be another name for y (Some writers use ≡ to mean congruence). P :⇔ Q means P is defined to be logically equivalent to Q. | cosh x := (1/2)(exp x + exp (−x)) A xor B :⇔ (A ∨ B) ∧ ¬(A ∧ B) |
| is defined as | |||
| everywhere | |||
| ≅ | congruence | △ABC ≅ △DEF means triangle ABC is congruent to (has the same measurements as) triangle DEF. | |
| is congruent to | |||
| geometry | |||
| { , } | set brackets | {a,b,c} means the set consisting of a, b, and c. | ℕ = { 1, 2, 3, …} |
| the set of … | |||
| set theory | |||
| { : } { | } | set builder notation | {x : P(x)} means the set of all x for which P(x) is true. {x | P(x)} is the same as {x : P(x)}. | {n ∈ ℕ : n2 <> |
| the set of … such that | |||
| set theory | |||
| ∅ { } | empty set | ∅ means the set with no elements. { } means the same. | {n ∈ ℕ : 1 < n2 < class="Unicode">∅ |
| the empty set | |||
| set theory | |||
| ∈ ∉ | set membership | a ∈ S means a is an element of the set S; a ∉ S means a is not an element of S. | (1/2)−1 ∈ ℕ 2−1 ∉ ℕ |
| is an element of; is not an element of | |||
| everywhere, set theory | |||
| ⊆ ⊂ | subset | (subset) A ⊆ B means every element of A is also element of B. (proper subset) A ⊂ B means A ⊆ B but A ≠ B. (Some writers use the symbol ⊂ as if it were the same as ⊆.) | (A ∩ B) ⊆ A ℕ ⊂ ℚ ℚ ⊂ ℝ |
| is a subset of | |||
| set theory | |||
| ⊇ ⊃ | superset | A ⊇ B means every element of B is also element of A. A ⊃ B means A ⊇ B but A ≠ B. (Some writers use the symbol ⊃ as if it were the same as ⊇.) | (A ∪ B) ⊇ B ℝ ⊃ ℚ |
| is a superset of | |||
| set theory | |||
| ∪ | set-theoretic union | (exclusive) A ∪ B means the set that contains all the elements from A, or all the elements from B, but not both. "A or B, but not both." (inclusive) A ∪ B means the set that contains all the elements from A, or all the elements from B, or all the elements from both A and B. "A or B or both". | A ⊆ B ⇔ (A ∪ B) = B (inclusive) |
| the union of … and union | |||
| set theory | |||
| ∩ | set-theoretic intersection | A ∩ B means the set that contains all those elements that A and B have in common. | {x ∈ ℝ : x2 = 1} ∩ ℕ = {1} |
| intersected with; intersect | |||
| set theory | |||
| Δ | symmetric difference | AΔB means the set of elements in exactly one of A or B. | {1,5,6,8} Δ {2,5,8} = {1,2,6} |
| symmetric difference | |||
| set theory | |||
| ∖ | set-theoretic complement | A ∖ B means the set that contains all those elements of A that are not in B. | {1,2,3,4} ∖ {3,4,5,6} = {1,2} |
| minus; without | |||
| set theory | |||
| ( ) | function application | f(x) means the value of the function f at the element x. | If f(x) := x2, then f(3) = 32 = 9. |
| of | |||
| set theory | |||
| precedence grouping | Perform the operations inside the parentheses first. | (8/4)/2 = 2/2 = 1, but 8/(4/2) = 8/2 = 4. | |
| parentheses | |||
| everywhere | |||
| f:X→Y | function arrow | f: X → Y means the function f maps the set X into the set Y. | Let f: ℤ → ℕ be defined by f(x) := x2. |
| from … to | |||
| set theory | |||
| o | function composition | fog is the function, such that (fog)(x) = f(g(x)). | if f(x) := 2x, and g(x) := x + 3, then (fog)(x) = 2(x + 3). |
| composed with | |||
| set theory | |||
| ℕ N | natural numbers | N means { 1, 2, 3, ...}, but see the article on natural numbers for a different convention. | ℕ = {|a| : a ∈ ℤ, a ≠ 0} |
| N | |||
| numbers | |||
| ℤ Z | integers | ℤ means {..., −3, −2, −1, 0, 1, 2, 3, ...} and ℤ+ means {1, 2, 3, ...} = ℕ. | ℤ = {p, -p : p ∈ ℕ} ∪ {0} |
| Z | |||
| numbers | |||
| ℚ Q | rational numbers | ℚ means {p/q : p ∈ ℤ, q ∈ ℕ}. | 3.14000... ∈ ℚ π ∉ ℚ |
| Q | |||
| numbers | |||
| ℝ R | real numbers | ℝ means the set of real numbers. | π ∈ ℝ √(−1) ∉ ℝ |
| R | |||
| numbers | |||
| ℂ C | complex numbers | ℂ means {a + b i : a,b ∈ ℝ}. | i = √(−1) ∈ ℂ |
| C | |||
| numbers | |||
| arbitrary constant | C can be any number, most likely unknown; usually occurs when calculating antiderivatives. | if f(x) = 6x² + 4x, then F(x) = 2x³ + 2x² + C | |
| C | |||
| integral calculus | |||
| ∞ | infinity | ∞ is an element of the extended number line that is greater than all real numbers; it often occurs in limits. | limx→0 1/|x| = ∞ |
| infinity | |||
| numbers | |||
| π | pi | π is the ratio of a circle's circumference to its diameter. Its value is 3.14159265... . | A = π r² is the area of a circle with radius r π radians = 180° π ≈ 22 / 7 |
| pi | |||
| Euclidean geometry | |||
| ||…|| | norm | || x || is the norm of the element x of a normed vector space. | || x + y || ≤ || x || + || y || |
| norm of length of | |||
| linear algebra | |||
| ∑ | summation |
|
|
| sum over … from … to … of | |||
| arithmetic | |||
| ∏ | product |
|
|
| product over … from … to … of | |||
| arithmetic | |||
| Cartesian product |
|
| |
| the Cartesian product of; the direct product of | |||
| set theory | |||
| ∐ | coproduct | ||
| coproduct over … from … to … of | |||
| category theory | |||
| ′ | derivative | f ′(x) is the derivative of the function f at the point x, i.e., the slope of the tangent to f at x. | If f(x) := x2, then f ′(x) = 2x |
| … prime derivative of | |||
| calculus | |||
| ∫ | indefinite integral or antiderivative | ∫ f(x) dx means a function whose derivative is f. | ∫x2 dx = x3/3 + C |
| indefinite integral of the antiderivative of | |||
| calculus | |||
| definite integral | ∫ab f(x) dx means the signed area between the x-axis and the graph of the function f between x = a and x = b. | ∫0b x2 dx = b3/3; | |
| integral from … to … of … with respect to | |||
| calculus | |||
| ∇ | gradient | ∇f (x1, …, xn) is the vector of partial derivatives (∂f / ∂x1, …, ∂f / ∂xn). | If f (x,y,z) := 3xy + z², then ∇f = (3y, 3x, 2z) |
| del, nabla, gradient of | |||
| calculus | |||
| ∂ | partial derivative | With f (x1, …, xn), ∂f/∂xi is the derivative of f with respect to xi, with all other variables kept constant. | If f(x,y) := x2y, then ∂f/∂x = 2xy |
| partial derivative of | |||
| calculus | |||
| boundary | ∂M means the boundary of M | ∂{x : ||x|| ≤ 2} = {x : ||x|| = 2} | |
| boundary of | |||
| topology | |||
| ⊥ | perpendicular | x ⊥ y means x is perpendicular to y; or more generally x is orthogonal to y. | If l ⊥ m and m ⊥ n then l || n. |
| is perpendicular to | |||
| geometry | |||
| bottom element | x = ⊥ means x is the smallest element. | ∀x : x ∧ ⊥ = ⊥ | |
| the bottom element | |||
| lattice theory | |||
| || | parallel | x || y means x is parallel to y. | If l || m and m ⊥ n then l ⊥ n. |
| is parallel to | |||
| geometry | |||
| ⊧ | entailment | A ⊧ B means the sentence A entails the sentence B, that is every model in which A is true, B is also true. | A ⊧ A ∨ ¬A |
| entails | |||
| model theory | |||
| ⊢ | inference | x ⊢ y means y is derived from x. | A → B ⊢ ¬B → ¬A |
| infers or is derived from | |||
| propositional logic, predicate logic | |||
| ◅ | normal subgroup | N ◅ G means that N is a normal subgroup of group G. | Z(G) ◅ G |
| is a normal subgroup of | |||
| group theory | |||
| / | quotient group | G/H means the quotient of group G modulo its subgroup H. | {0, a, 2a, b, b+a, b+2a} / {0, b} = {{0, b}, {a, b+a}, {2a, b+2a}} |
| mod | |||
| group theory | |||
| quotient set | A/~ means the set of all ~ equivalence classes in A. | ||
| set theory | |||
| ≈ | isomorphism | G ≈ H means that group G is isomorphic to group H | Q / {1, −1} ≈ V, where Q is the quaternion group and V is the Klein four-group. |
| is isomorphic to | |||
| group theory | |||
| approximately equal | x ≈ y means x is approximately equal to y | π ≈ 3.14159 | |
| is approximately equal to | |||
| everywhere | |||
| ~ | same order of magnitude | m ~ n, means the quantities m and n have the general size. (Note that ~ is used for an approximation that is poor, otherwise use ≈ .) | 2 ~ 5 8 × 9 ~ 100 but π2 ≈ 10 |
| roughly similar poorly approximates | |||
| Approximation theory | |||
| <,> | inner product | <x,y> means the inner product between x and y, as defined in an inner product space. | The standard inner product between two vectors x = (2, 3) and y = (-1, 5) is: |
| inner product of | |||
| vector algebra | |||
| ⊗ | tensor product | V ⊗ U means the tensor product of V and U. | {1, 2, 3, 4} ⊗ {1,1,2} = {{1, 2, 3, 4}, {1, 2, 3, 4}, {2, 4, 6, 8}} |
| tensor product of | |||
| linear algebra |
 means a1 + a2 + … + an.
means a1 + a2 + … + an. = 12 + 22 + 32 + 42
= 12 + 22 + 32 + 42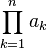 means a1a2···an.
means a1a2···an. = (1+2)(2+2)(3+2)(4+2)
= (1+2)(2+2)(3+2)(4+2) means the set of all
means the set of all 